来源:长盛基金
在统计学中,有哪些常见的谬误?
● 在分组比较中都占优势的一方,为什么在总评中反而成为失势的一方?
● 小红热爱音乐,她更可能是琴师还是会计?
● 把一个样本从一个组移去另一个组,怎么会同时提升两个组的平均值?
今天小盛就带大家看看关于统计学谬误的那些事儿~
辛普森悖论
辛普森悖论,指的是在分组比较中都占优势的一方,在总评中反而成为失势的一方。
1996年,Appleton, French, 和 Vanderpump三位学者做过一个探索吸烟和死亡率的关系实验,具体数据如下:
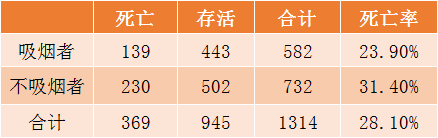
实验结果表明,非吸烟人群死亡率高于吸烟人群,但这明显违背了医学对我们传达出的吸烟有害健康的常识。接下来,三位学者尝试按照年龄对人群进行分组,则得到另一个截然不同的结果。
从上图我们可以看到,按年龄划分后,几乎所有子群体中,吸烟者的死亡率都要高于非吸烟者,这就是典型的辛普森悖论。由此可以看出,在分析吸烟和死亡率之间的关系时,年龄似乎是一个重要的应该被考虑进去的因素。
因此,辛普森悖论告诉我们,不能简单的将分组数据汇总相加。我们需要仔细观察分组数据的特征,想一想有没有可能被表面的数据掩盖了背后的真相。这是我们能够从辛普森悖论中学到的教训。
基本比率谬误
关于基本比率谬误我们可以来先来看两个问题:
➤ 问题一:小明的钢琴弹得很好,在他学琴的过程中,他的爸爸教了他很多技巧。那么小明爸爸的职业更可能是:A大学音乐老师 B销售人员
➤问题二:小红家里很有钱,平时身穿名贵时装,用着高档化妆品,背着几万块的包。一天小红走进商场,她买的东西里更可能有:A香奈儿的香水 B矿泉水
以上两个问题,如果你有一道选择了A,恭喜你,你已掉进了基本比率谬误的陷阱里。如果你都选择的B选项,很不错,你没有犯最简单的基本比率谬误。
基本比率谬误,指的是人往往会通过代表性来评估概率,而忽视了基本比率。所谓通过代表性评估概率,就是因为某个个体的特征与某个群体相似,就认为个体很可能来自该群体,却忽略了该群体本身出现的概率实际上很低。
罗杰斯现象
罗杰斯现象指的是,在做数据统计时,如果把一个样本从一个组移去另一个组,会同时提升两个组的平均值。
一些读者看到这句话,可能会觉得不可思议。让我通过一个例子来给大家解释一下。假设有6个人,分别为40、50、60、70、80、和90岁。现在将他们分为两组。第一组包括40岁和50岁的两人,因此组平均年龄为45岁。剩下的归入第二组,因此组平均年龄为75岁。
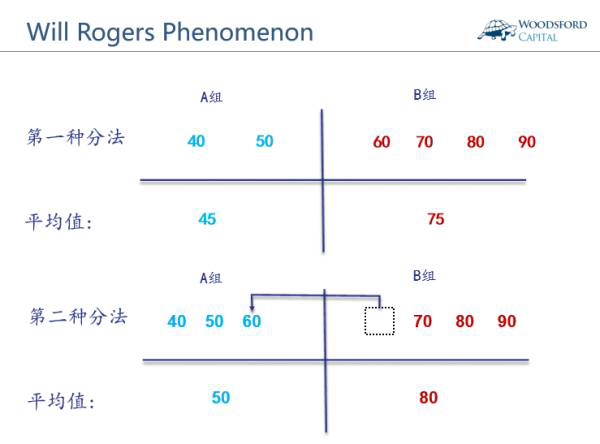
现在把第二组中的那位60岁的人,移去第一组。移过去以后,第一组的平均年龄变为50岁,而第二组的平均年龄变为80岁。两组的平均年龄都上升了。
罗杰斯现象,导致我们在医学领域产生一些容易让人混淆的,似是而非的结论。
举例来说,前列腺特异抗原测试(PSA测试)可以帮助我们诊断前列腺癌。有了PSA测试这项技术以后,很多人在年纪轻轻时也能通过该测试确诊自己是否患上前列腺癌。这部分人,就被移出“健康”人群,归入“患者”人群。
由于这个归类的变化,导致患上前列腺癌的“患者”人群,以及“健康”人群的平均寿命都得到了提高。因为“健康”人群中被移去一部分癌症患者,而这些癌症患者属于“轻度病患”(前列腺癌的致死率很低),因此“健康”和“患者”两个人群的寿命平均值均得到了提升,让人误以为PSA测试能够帮助我们延长寿命。
在信息不断膨胀的现代社会中,可以说,统计陷阱比比皆是,而且还不断推陈出新,投资中你的收益被平均、工作中你的工资被平均等等现象都是统计学谬误的体现。因此,我们解读现实中各种各样的统计结果时,务必要多一些警惕的心理与多一点批判的眼光。同时,提高自己的科学知识水平,保持不断学习的习惯,是让自己变得更聪明的唯一途径。
郑重声明:本文版权归原作者所有,转载文章仅为传播更多信息之目的,如作者信息标记有误,请第一时间联系我们修改或删除,多谢。



